Rewrite 9 5/2 in radical form – In the realm of mathematics, understanding radical form is essential. It holds significance in various fields, and converting mixed numbers into radical form is a crucial skill. This guide delves into the conversion of 9 5/2 into radical form, providing a step-by-step approach and exploring the practical applications of radical form in real-world scenarios.
We will also cover the basic operations that can be performed on radicals, such as addition, subtraction, and multiplication. By the end of this guide, you will have a thorough understanding of radical form and its applications.
Understanding Radical Form: Rewrite 9 5/2 In Radical Form

In mathematics, a radical form is a way of expressing a number as the root of another number. Radicals are used to represent numbers that are not perfect squares or cubes, such as the square root of 2 or the cube root of 3. Radical form is significant because it allows us to perform operations on these numbers in a more convenient way.
Types of Radicals
There are two main types of radicals: square roots and cube roots. A square root is the root of a number that is raised to the power of 2, while a cube root is the root of a number that is raised to the power of 3. For example, the square root of 4 is 2, and the cube root of 8 is 2.
Properties of Radicals
Radicals have several important properties that can be used to simplify and solve equations. Some of the most important properties of radicals include:
- The square root of a positive number is always positive.
- The cube root of a positive number is always positive.
- The square root of a negative number is not a real number.
- The cube root of a negative number is a real number.
- The square root of a product is equal to the product of the square roots.
- The cube root of a product is equal to the product of the cube roots.
- The square root of a quotient is equal to the quotient of the square roots.
- The cube root of a quotient is equal to the quotient of the cube roots.
Converting Mixed Numbers to Radical Form
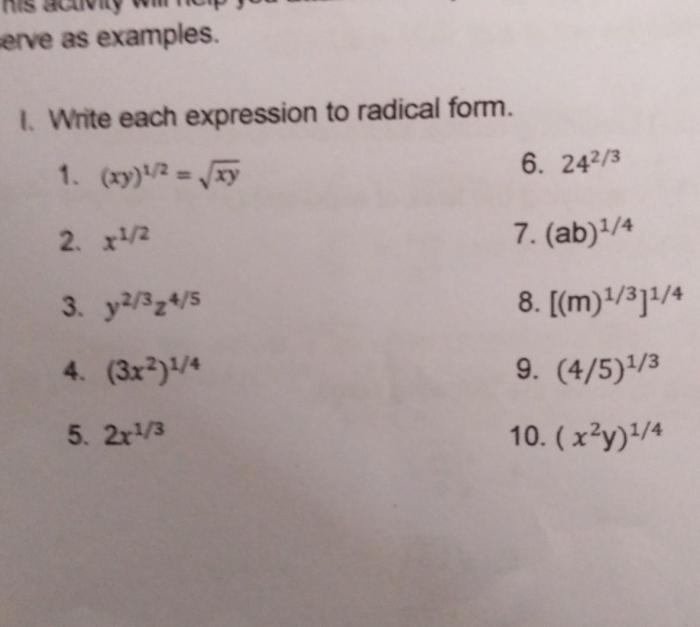
Mixed numbers combine whole numbers and fractions. To convert a mixed number into radical form, follow these steps:
- Multiply the whole number by the denominator of the fraction.
- Add the numerator of the fraction to the product obtained in step 1.
- Place the result obtained in step 2 under the radical sign, with the denominator of the fraction as the index.
Examples:
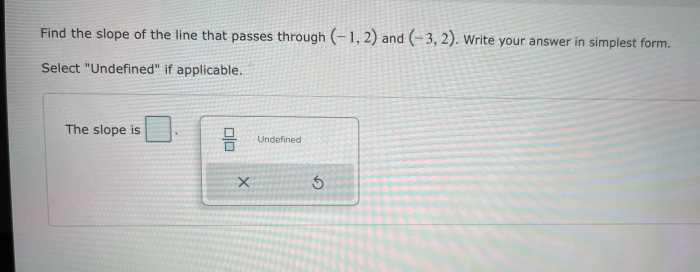
- Convert 2 1/2 to radical form:
(2 x 2) + 1 = 5 under the square root (√) sign with an index of 2
- Convert 3 3/4 to radical form:
(3 x 4) + 3 = 15 under the square root (√) sign with an index of 4
Specific Case: 9 5/2

Let’s delve into the specific mixed number 9 5/2 and explore how to convert it into radical form.Converting a mixed number to radical form involves two steps:
- Expressing the fractional part as a radical.
- Multiplying the whole number part by the radical expression.
Expressing the Fractional Part as a Radical, Rewrite 9 5/2 in radical form
In this case, the fractional part is 5/
To express it as a radical, we follow the rule:
$$\sqrt\fracab = \frac\sqrta\sqrtb$$Applying this rule, we get:$$\sqrt\frac52 = \frac\sqrt5\sqrt2$$
Multiplying the Whole Number Part by the Radical Expression
Now, we multiply the whole number part, 9, by the radical expression we obtained:$$9 \times \frac\sqrt5\sqrt2$$Simplifying the expression, we get the radical form of 9 5/2:$$9 \sqrt\frac52$$
Rewriting 9 5/2 in radical form can be a bit tricky, but it’s definitely doable. And while we’re on the topic of healthcare professionals, have you ever wondered if a CNA needs a stethoscope? If you’re curious, you can find out more about it here . Anyway, back to our original topic, 9 5/2 can be written as a radical expression using the formula √(a/b) = √a/√b.
So, 9 5/2 = √(9 2)/√2 = 3√2.
Mathematical Operations with Radicals
In the realm of radicals, we can perform a suite of fundamental operations, namely addition, subtraction, and multiplication. These operations are essential for manipulating radical expressions and solving mathematical equations.
Addition and Subtraction of Radicals
When adding or subtracting radicals, we must ensure that the radicals have the same index and radicand. If they do, we can simply add or subtract their coefficients while leaving the radical expression unchanged.
For instance, 3√2 + 5√2 = 8√2 and 7√5
2√5 = 5√5.
Multiplication of Radicals
Multiplying radicals involves multiplying their coefficients and multiplying their radicands using the rules of exponents. If the radicands are the same, we can simplify the expression by adding their exponents.
For example, (2√3)(5√6) = 10√18 = 10√(9
- 2) = 10√9
- √2 = 30√2.
Application to 9 5/2
To express 9 5/2 in radical form, we can rewrite it as 9 + 5/ 2. Since the radicand is a sum, we can use the rule for adding radicals:
9 + 5/2 = √9 + √(5/2) = 3 + √(5/2).
Applications of Radical Form
The radical form, such as the one representing 9 5/2, has numerous applications across various fields, including geometry, physics, and engineering. In these fields, radical form provides a concise and efficient way to represent and manipulate complex mathematical expressions involving square roots.
Geometry
In geometry, radical form is used to calculate the lengths of sides and diagonals of shapes, such as triangles, squares, and circles. For example, the length of the diagonal of a square with side length 5 can be expressed as 5√2, where √2 represents the square root of 2.
Physics
In physics, radical form is used to describe the motion of objects, such as the velocity and acceleration of a projectile. For example, the velocity of a projectile launched at an angle θ with an initial velocity v can be expressed as v(cosθ, sinθ), where cosθ and sinθ represent the cosine and sine of the angle θ, respectively.
Engineering
In engineering, radical form is used to calculate the stresses and strains in structures, such as bridges and buildings. For example, the stress on a beam can be expressed as σ = F/A, where F is the force applied to the beam and A is the cross-sectional area of the beam.
Clarifying Questions
What is radical form?
Radical form is a way of expressing a number as the root of another number.
How do I convert a mixed number to radical form?
To convert a mixed number to radical form, multiply the whole number by the denominator of the fraction, add the numerator, and place the result under the square root of the denominator.
What are the applications of radical form?
Radical form has applications in geometry, physics, and engineering. For example, it is used to calculate the length of a diagonal of a square or the distance between two points on a circle.