Sets and venn diagrams assignment – Embarking on an exploration of sets and Venn diagrams, this comprehensive assignment delves into the fundamental concepts, applications, and problem-solving techniques associated with these mathematical tools. By unraveling the intricacies of sets and Venn diagrams, we gain a deeper understanding of organizing, representing, and analyzing data, equipping us to tackle real-world challenges with precision and efficiency.
Throughout this assignment, we will delve into the concept of sets, exploring their properties, operations, and relationships. We will then venture into the realm of Venn diagrams, uncovering their power in visualizing and comprehending set relationships. Finally, we will culminate our journey by examining the practical applications of sets and Venn diagrams in various fields, highlighting their versatility and problem-solving prowess.
Sets
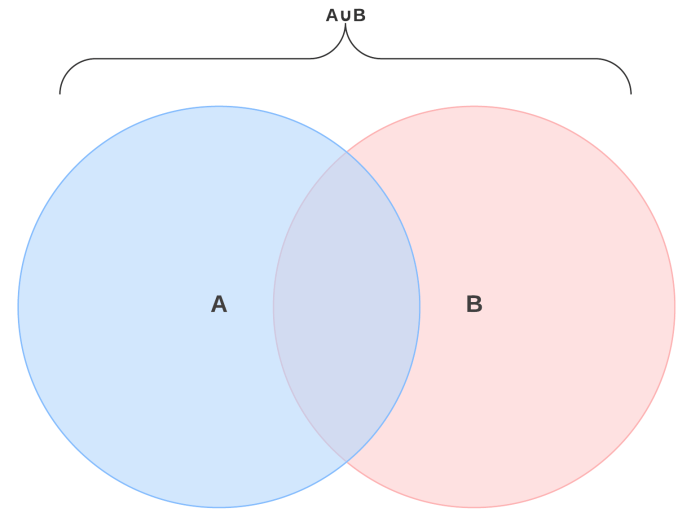
Sets are mathematical structures that represent unordered collections of distinct elements. They are often used to organize and represent data in a clear and concise way.
Examples of sets include the set of all natural numbers, the set of all vowels in the English alphabet, and the set of all students in a particular class.
Operations on Sets, Sets and venn diagrams assignment
- Union (A ∪ B):The union of two sets A and B is a new set that contains all the elements that are in either A or B.
- Intersection (A ∩ B):The intersection of two sets A and B is a new set that contains all the elements that are in both A and B.
- Difference (A- B): The difference of two sets A and B is a new set that contains all the elements that are in A but not in B.
- Complement (AC): The complement of a set A is a new set that contains all the elements that are not in A.
Venn Diagrams: Sets And Venn Diagrams Assignment
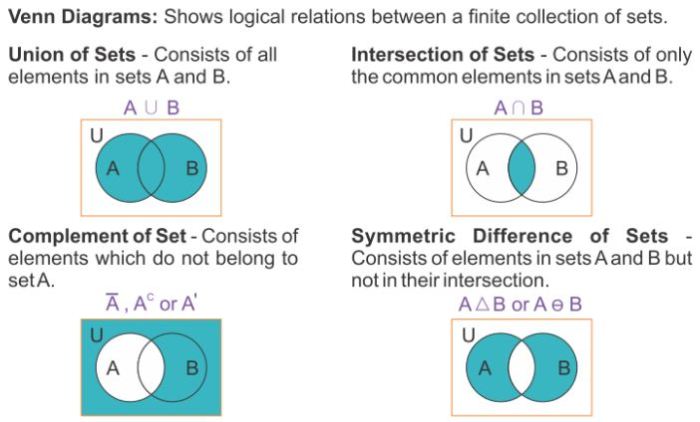
Venn diagrams are graphical representations of sets and their relationships. They use overlapping circles to represent the sets and the areas where the circles overlap represent the elements that are in both sets.
For example, a Venn diagram could be used to represent the sets of students who like math and the students who like science. The overlapping area would represent the students who like both math and science.
Using Venn Diagrams to Represent Sets
To use a Venn diagram to represent sets, follow these steps:
- Draw a circle for each set.
- Label each circle with the name of the set.
- Shade the area of the Venn diagram that represents the elements that are in both sets.
Applications of Sets and Venn Diagrams
Sets and Venn diagrams are used in a wide variety of applications, including:
- Computer science:Sets are used to represent data structures such as arrays and linked lists. Venn diagrams are used to represent the relationships between different sets of data.
- Mathematics:Sets are used to define mathematical concepts such as functions and limits. Venn diagrams are used to visualize the relationships between different sets of numbers.
- Statistics:Sets are used to represent the outcomes of experiments. Venn diagrams are used to visualize the relationships between different sets of outcomes.
FAQ
What is the purpose of a Venn diagram?
A Venn diagram is a graphical representation that illustrates the relationships between different sets. It helps visualize the overlapping and non-overlapping elements of sets, making it easier to understand their intersections, unions, and complements.
How can I use sets to solve problems?
Sets can be used to model real-world situations and solve problems by organizing and manipulating data. By representing elements as members of sets and applying set operations, we can simplify complex problems and derive logical conclusions.
What are the benefits of using sets and Venn diagrams?
Sets and Venn diagrams offer several benefits, including improved data organization, clear visualization of relationships, simplified problem-solving, and enhanced communication of mathematical ideas.