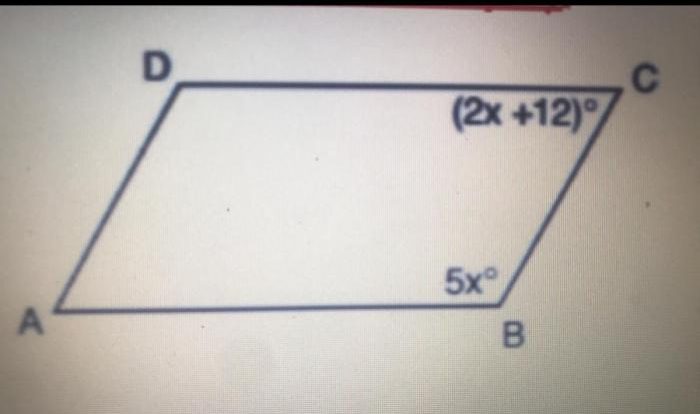
Practice points lines and planes 1 2 delve into the fascinating world of geometry, exploring the fundamental concepts of lines and planes, their relationships, and their applications in real-life scenarios. Embark on a journey of discovery as we unravel the intricacies of these geometric entities, unraveling their properties and significance.
From understanding the dimensionality of lines and planes to deciphering the nuances of point-line and line-plane relationships, this exploration promises a comprehensive understanding of the foundational principles of geometry.
1. Lines and Planes

In geometry, a line is a one-dimensional figure that extends infinitely in both directions. A plane is a two-dimensional figure that extends infinitely in all directions.
Lines and planes are fundamental geometric concepts that play a crucial role in many areas of mathematics and science. They are used to represent objects in the real world, such as roads, buildings, and landscapes.
Properties of Lines and Planes
- Lines are one-dimensional and have no width or height.
- Planes are two-dimensional and have no thickness.
- Lines and planes can intersect at a single point.
Examples of Lines and Planes in Everyday Life
- Roads and highways are examples of lines.
- Walls and floors are examples of planes.
- The surface of a lake or ocean is an example of a plane.
2. Point-Line Relationship
A point can be related to a line in several ways:
Collinear Points
Collinear points are points that lie on the same line. They are said to be “on the line”.
Points that Lie on a Line
A point that lies on a line is a point that is contained within the line. It is said to be “on the line”.
Examples of Point-Line Relationships in Real-World Scenarios, Practice points lines and planes 1 2
- The points on a ruler are collinear.
- The vertices of a triangle are points that lie on the sides of the triangle.
- The points on the circumference of a circle are points that lie on the circle.
3. Line-Plane Relationship: Practice Points Lines And Planes 1 2
A line can intersect a plane in several ways:
Parallel Lines
Parallel lines are lines that do not intersect. They are said to be “parallel to each other”.
Perpendicular Lines
Perpendicular lines are lines that intersect at a right angle. They are said to be “perpendicular to each other”.
Intersecting Lines
Intersecting lines are lines that intersect at a point. They are said to be “intersecting”.
Examples of Line-Plane Relationships in Architectural Structures and Natural Formations
- The walls and floors of a building are examples of planes that intersect at right angles.
- The sides of a pyramid are examples of planes that intersect at a point.
- The layers of rock in a canyon are examples of planes that are parallel to each other.
4. Parallel and Perpendicular Lines
Definition of Parallel Lines
Parallel lines are lines that do not intersect. They are said to be “parallel to each other”.
Definition of Perpendicular Lines
Perpendicular lines are lines that intersect at a right angle. They are said to be “perpendicular to each other”.
Properties of Parallel and Perpendicular Lines
- Parallel lines have the same slope.
- Perpendicular lines have slopes that are negative reciprocals of each other.
- Parallel lines never intersect.
- Perpendicular lines intersect at a single point.
Methods for Constructing Parallel and Perpendicular Lines Using Geometric Tools
- Parallel lines can be constructed using a ruler and protractor.
- Perpendicular lines can be constructed using a compass and straightedge.
FAQ Summary
What is the difference between a line and a plane?
A line is a one-dimensional geometric figure that extends infinitely in both directions, while a plane is a two-dimensional figure that extends infinitely in all directions.
What is the relationship between a point and a line?
A point can lie on a line, be collinear with the line (lie on the same line), or be skew to the line (not lie on the same line and not intersect it).
What is the relationship between a line and a plane?
A line can intersect a plane at a single point, be parallel to the plane (never intersect it), or be perpendicular to the plane (intersect it at a right angle).