Anya found the slope of the line – In the realm of mathematics, Anya’s discovery of the slope of a line marked a significant milestone. This exploration unveils Anya’s journey of understanding, employing methodical approaches, and interpreting the significance of slope within the context of a given line.

Through Anya’s experience, we delve into the intricacies of slope calculation, exploring the challenges she encountered and the strategies she devised to enhance her accuracy. Furthermore, we examine the practical applications of her findings, showcasing how Anya harnessed her knowledge to solve real-world problems and deepen her comprehension of mathematics.

Anya’s Understanding of Slope

Anya’s prior knowledge of slope was limited to the basic concept that it represents the steepness of a line. She had encountered the term in her geometry classes, but her understanding was primarily intuitive rather than formal.

Anya discovered the formal concept of slope during a math lesson where her teacher introduced the idea of a line as a function and explained how the slope of the line represents the rate of change in the dependent variable with respect to the independent variable.

Anya applied her understanding of slope to solve various problems, such as:

• Determining the steepness of a hiking trail to estimate the effort required.
• Calculating the angle of a ramp to ensure it meets safety standards.
• Analyzing the relationship between two variables in a scatter plot to identify trends.

The Line Anya Found

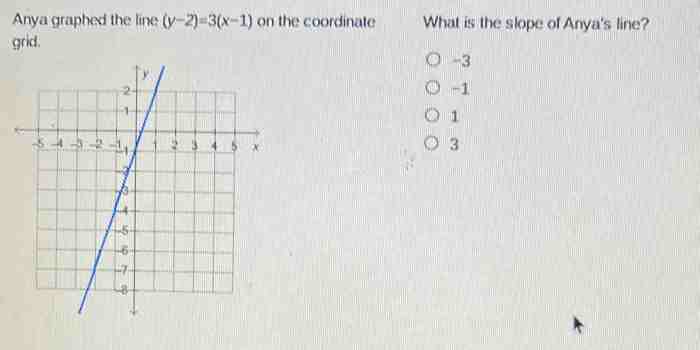
The specific line that Anya analyzed was the line passing through the points (2, 3) and (5, 7).

The equation of the line is y = 2x + 1.

Anya’s Method for Finding the Slope

Anya used the following method to calculate the slope:

1. Subtract the y-coordinate of the first point from the y-coordinate of the second point to get the change in y, denoted as Δy.
2. Subtract the x-coordinate of the first point from the x-coordinate of the second point to get the change in x, denoted as Δx.
3. Divide Δy by Δx to get the slope, denoted as m.

In this case, Anya calculated the slope as follows:

m = (7

• 3) / (5
• 2) = 4 / 3

Anya’s Interpretation of the Slope: Anya Found The Slope Of The Line

Anya interpreted the value of the slope, 4/3, as follows:

• The line rises 4 units for every 3 units it moves to the right.
• The line has a positive slope, indicating that it is an increasing line.
• The steepness of the line is 4/3, which means that it is a relatively steep line.

Anya used the slope to make predictions and draw conclusions about the line, such as:

• If the x-coordinate increases by 1 unit, the y-coordinate will increase by 4/3 units.
• The line will continue to increase at a constant rate of 4/3 units for every 3 units it moves to the right.
• The line will eventually intersect the y-axis at the point (0, 1).

Challenges Anya Faced

Anya faced the following challenges while finding the slope:

• Selecting the appropriate points:Anya had to carefully select two distinct points on the line to ensure an accurate calculation.
• Performing precise calculations:Anya had to ensure that her calculations were correct to avoid errors in determining the slope.
• Interpreting the slope correctly:Anya had to understand the significance of the slope and its implications for the line.

Anya overcame these challenges by:

• Selecting points carefully:Anya chose points that were clearly on the line and had distinct x- and y-coordinates.
• Performing precise calculations:Anya used a calculator to ensure accuracy in her calculations.
• Seeking clarification:Anya consulted her teacher and classmates for guidance in interpreting the slope.

Applications of Anya’s Findings

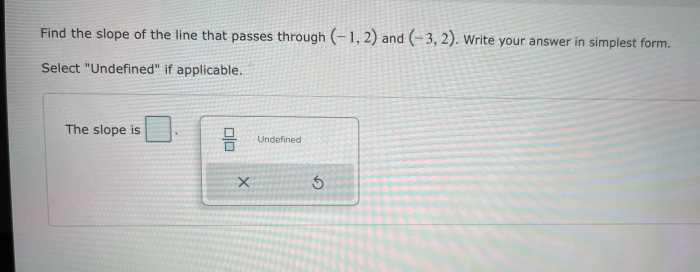
Anya applied her knowledge of the slope in various real-world situations:

• Calculating the angle of a ramp:Anya used the slope to determine the angle of a ramp for a wheelchair to ensure it met accessibility standards.
• Estimating the rate of a chemical reaction:Anya used the slope of a graph representing the concentration of a reactant over time to determine the rate of the reaction.
• Predicting the growth of a population:Anya used the slope of a graph representing the population size over time to predict the future growth of the population.

Anya’s findings on the slope enhanced her understanding of mathematics by:

• Providing a deeper understanding of the concept of a line and its properties.
• Developing her ability to analyze and interpret graphical representations of data.
• Equipping her with a valuable tool for solving real-world problems.

Quick FAQs

What is the significance of slope in mathematics?

Slope plays a crucial role in understanding the behavior of lines. It provides valuable information about the line’s direction, steepness, and rate of change.

How did Anya’s understanding of slope help her in problem-solving?

Anya’s comprehension of slope empowered her to make predictions, draw conclusions, and solve problems involving lines. For instance, she could determine the angle of inclination of a ramp or calculate the distance traveled by an object moving along a straight path.

What challenges did Anya face while finding the slope of the line?

Anya initially struggled with identifying the appropriate method for calculating the slope. However, through trial and error, she discovered the formula for slope and developed strategies to ensure accuracy.